Ideal Polymer Chains:
Distribution of End-to-End Distance

A linear flexible polymer chain in the melt- or theta-state can be modeled as a random flight in three dimensions where all intermolecular interactions between polymer chains are neglected which is equivalent to the Gaussian chain model. It is assumed that each bond has a constant length l, which is the mean length of a statistical repeat unit.¹ These bonds are allowed to freely rotate about the backbone. Then the space available to each bond vector (r) is equal to a sphere of radius l and the bond probability distribution in continuous space can be written as a delta function of bond length:

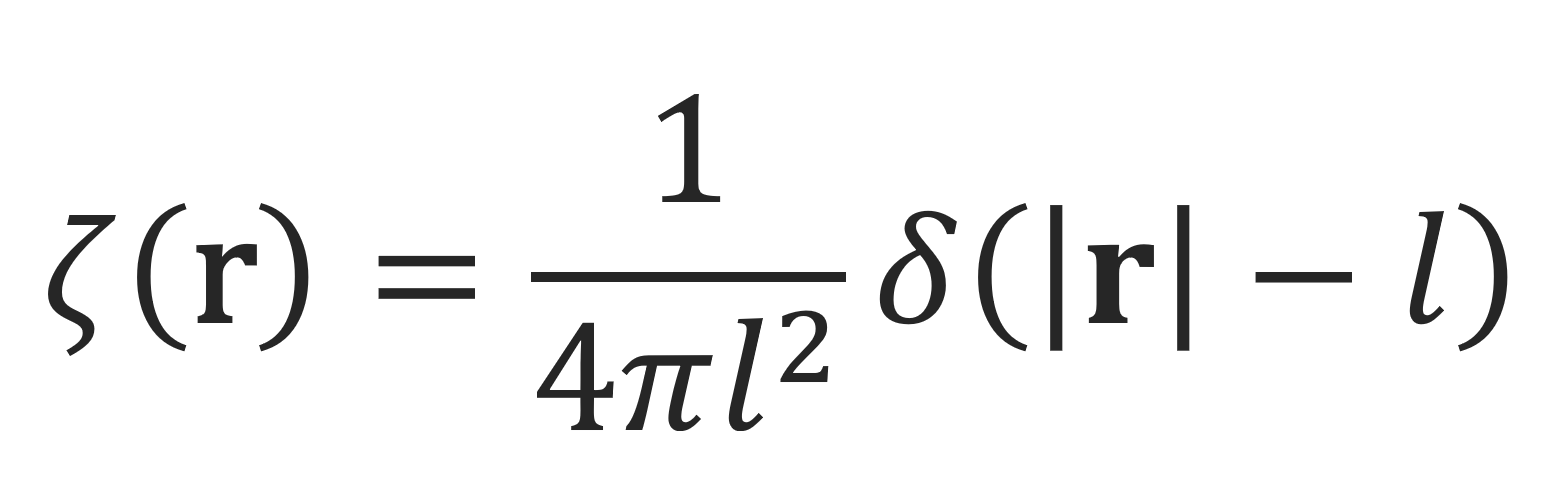
Since the N statistical bonds of this freely-linked chain do not interfere with one another, the probability of a random configuration of N bond vectors {r_i} is simply the product of the N bond probabilities:

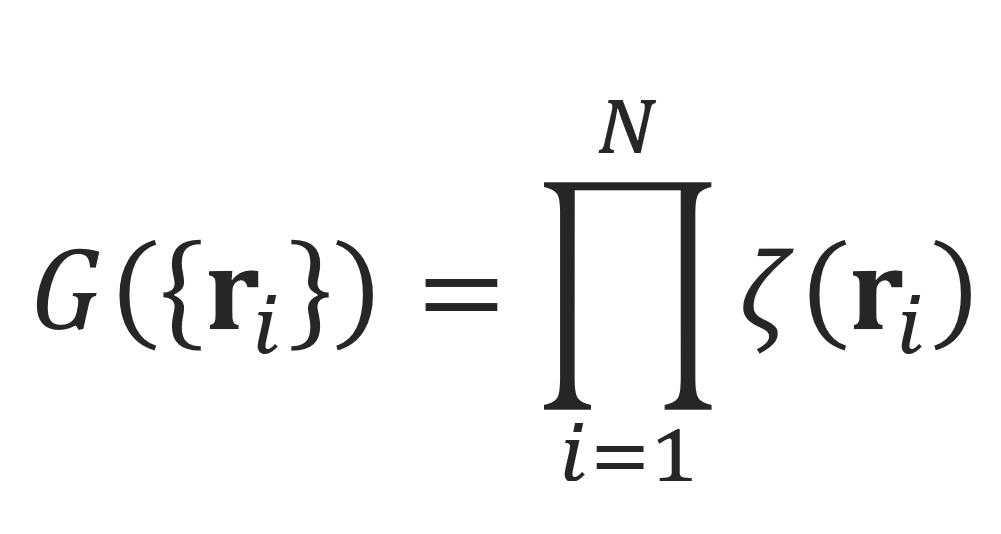
The conformation of a chain is determined by the N bond vectors {r_i} = r₀...r_N and the sum of the bond vectors is equal to the end-to-end vector R of the polymer chain:

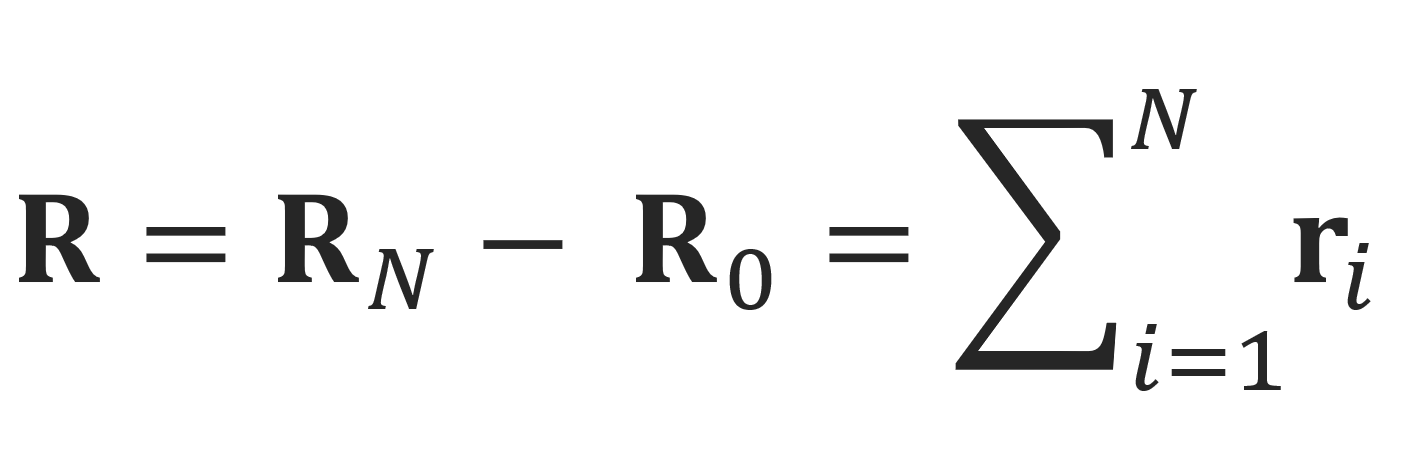
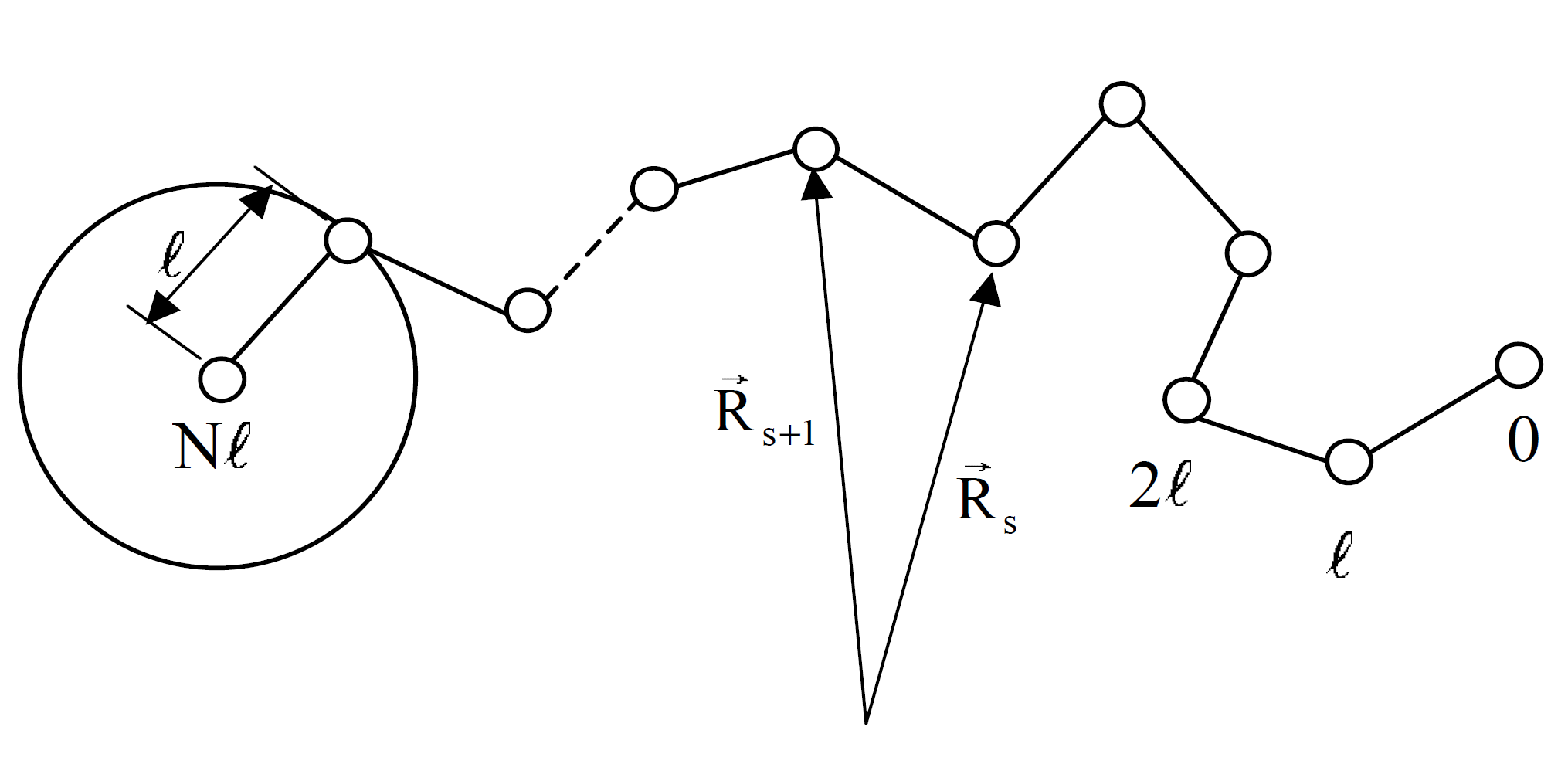
The probability G(R) of finding an end-to-end vector R = R_N – R₀ can be obtained by integration over all possible conformations with fixed end-to-end vector R:^2-4

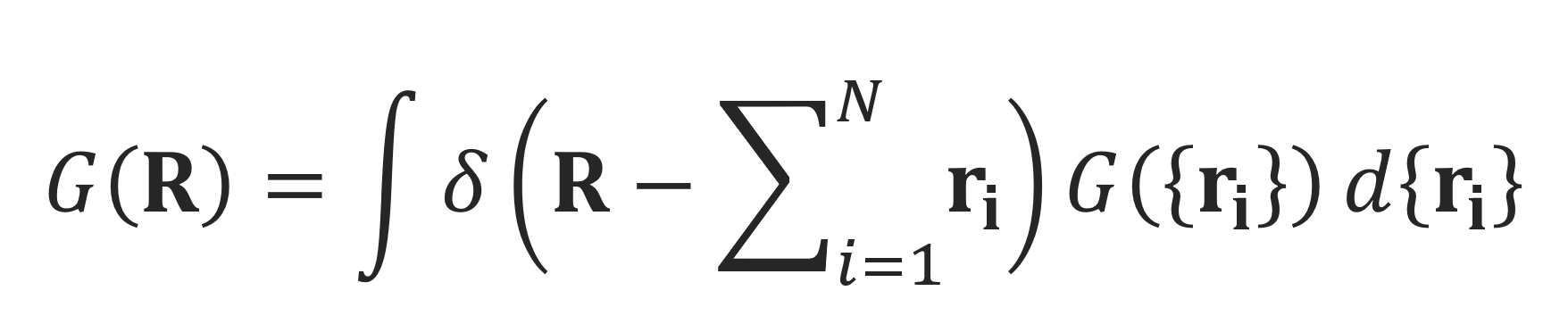
Using Dirichlet’s cutoff integral or Fourier representation of the three-dimensional Dirac delta function,³

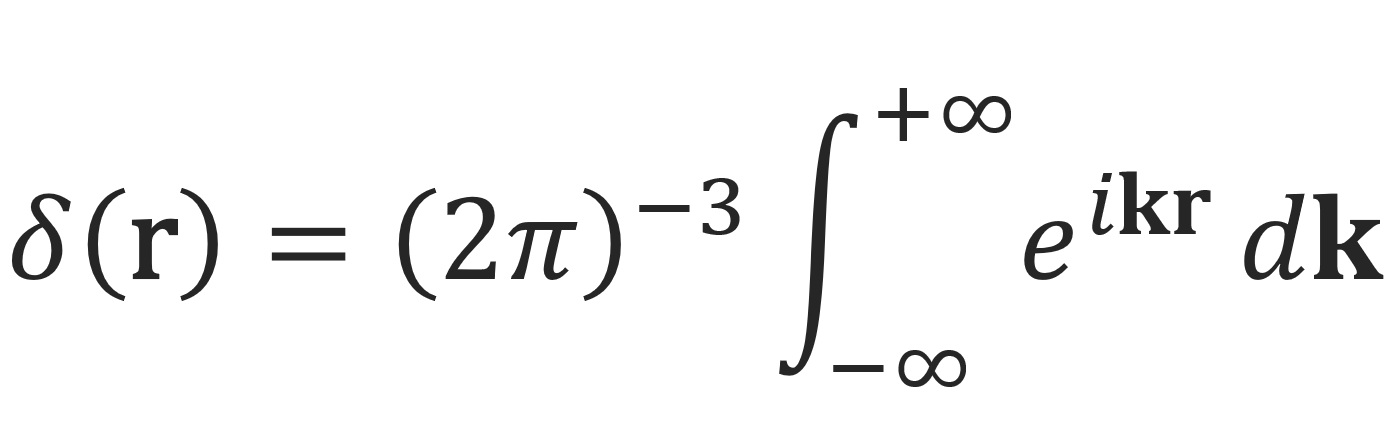
the equation for G(R) can be rewritten in the form

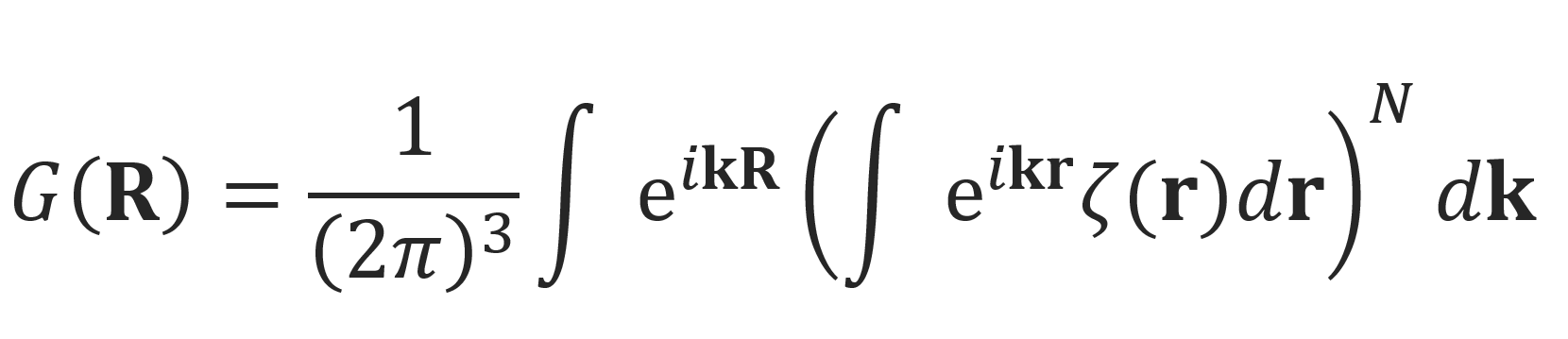
The inner integral can be easily evaluated when introducing polar coordinates (r, θ, φ) with the z axis in the direction of k:

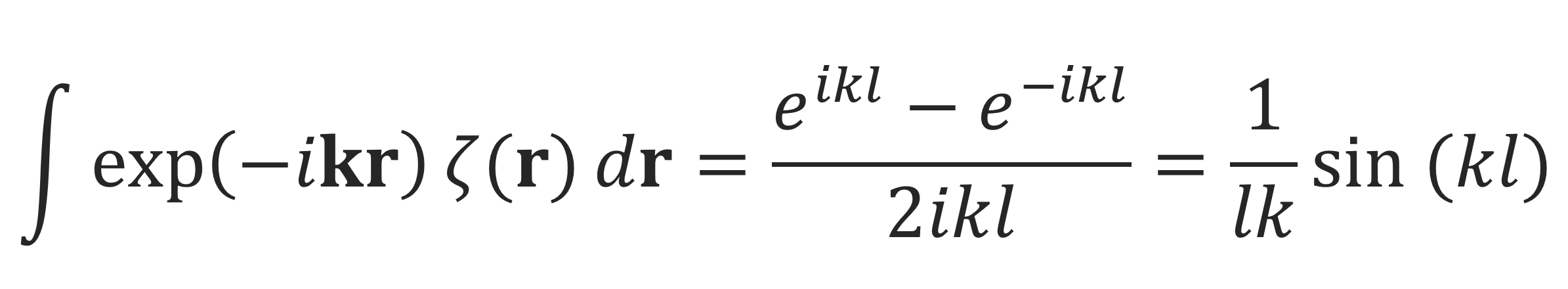
Then G(R) may be rewritten in the form

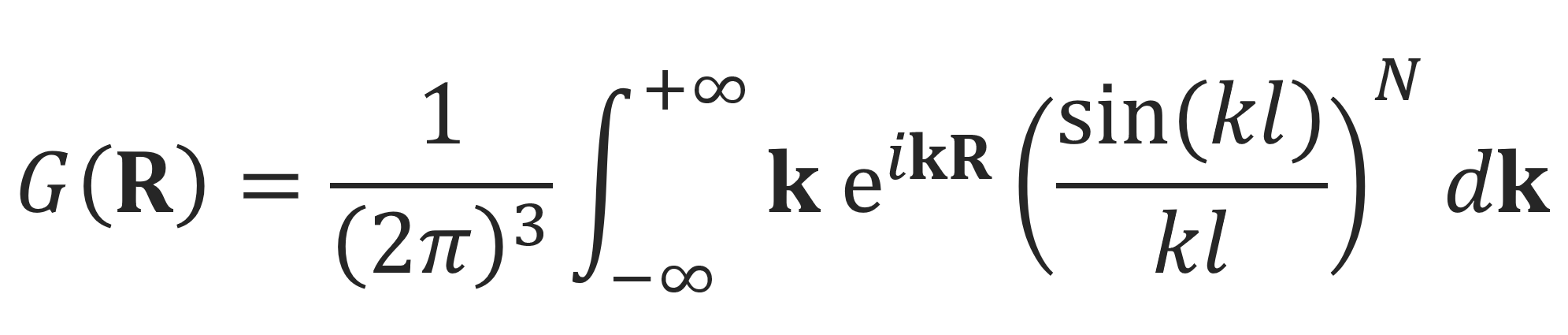
or

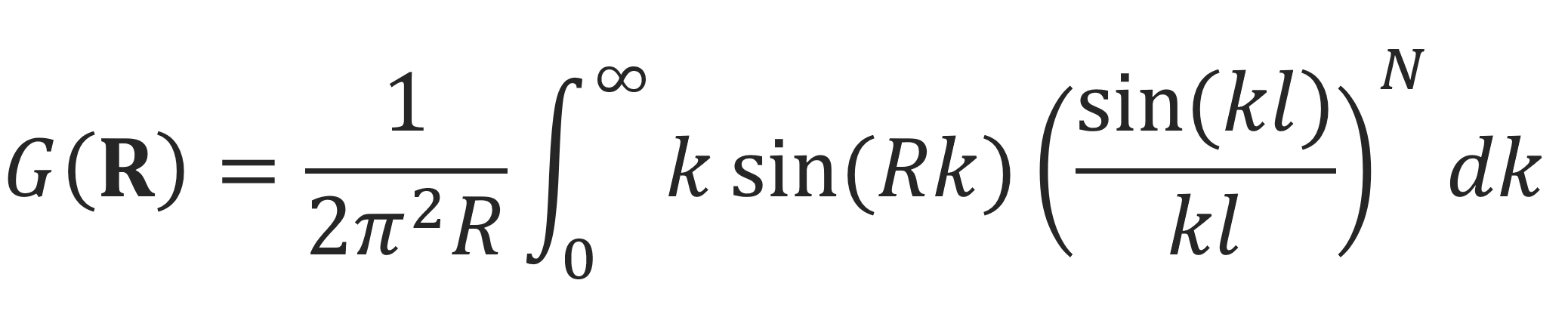
Exact solutions were obtained by several scientists using different mathematical methods.^5-9 The results can be expressed as a series in k,³

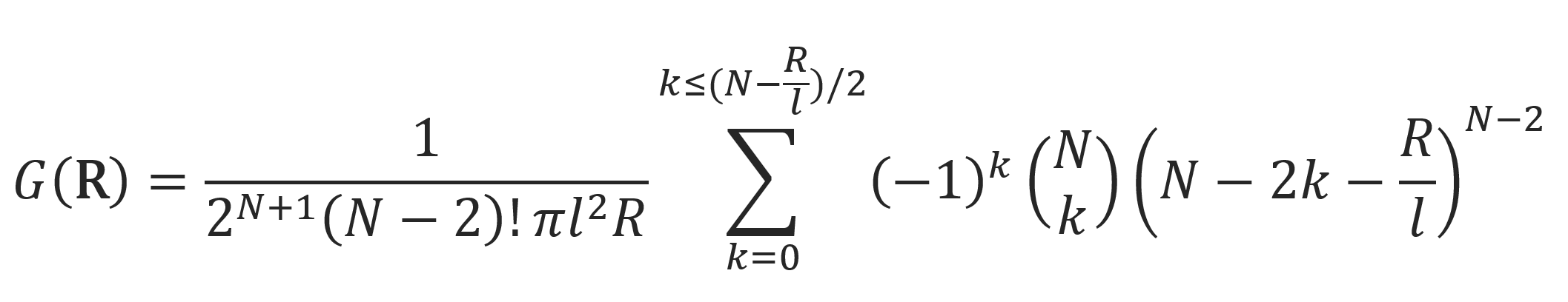
For long chains (N >> 1), the calculation of the distribution of the end-to-end vector is very cumbersome and thus not useful for most practical problems. For this reason, several asymptotic solutions have been suggested.
For very long chains (N → ∞), [sin(kl) / kl)]^N becomes very small. For this case, we may expand sin(kl) in a Taylor series around k = 0,

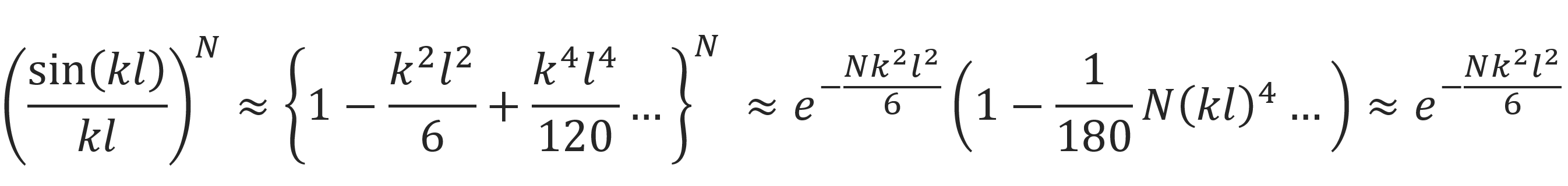
Using this expression, the probability density may be written in the form

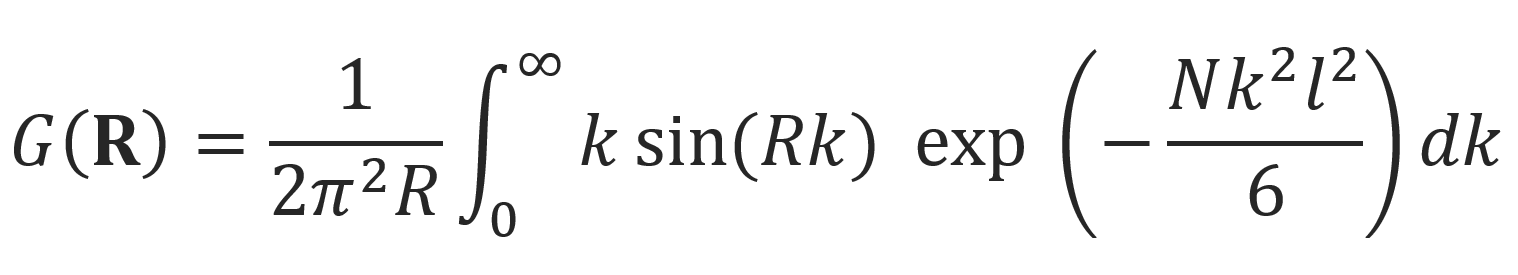
Integration in this equation can be easily performed, which yields the well-known probability distribution of a random walk in three dimensions:

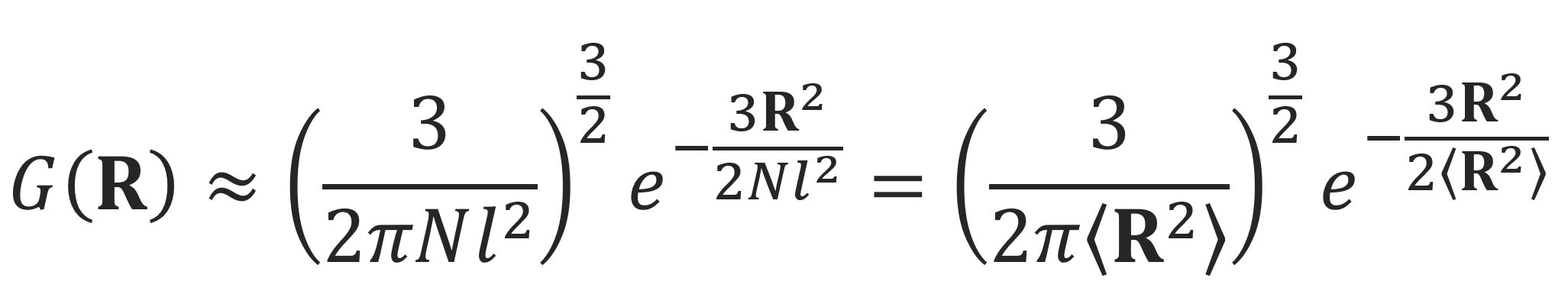
This probability distribution is an excellent approximation to the exact solution for small end-to-end distances (R / Nl << 1) and long polymer chains (N >> 1). For stretched chains, however, the results will noticeably deviate from the exact probability distribution. For this case, we have to include higher-order terms which yields upon integration^3,4

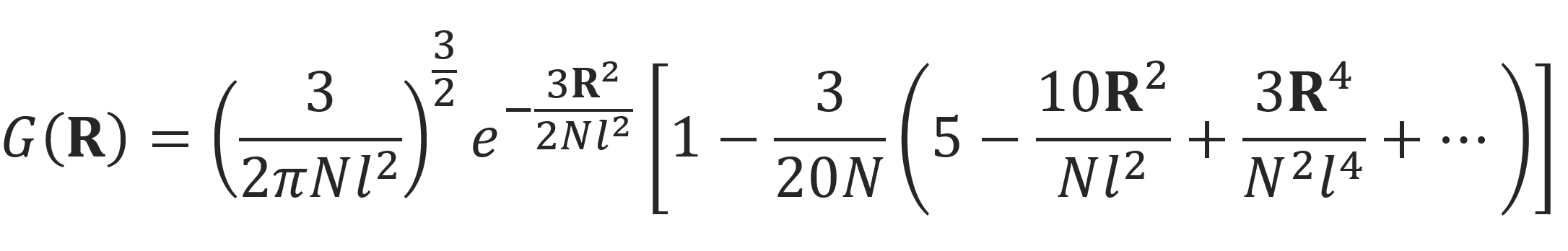
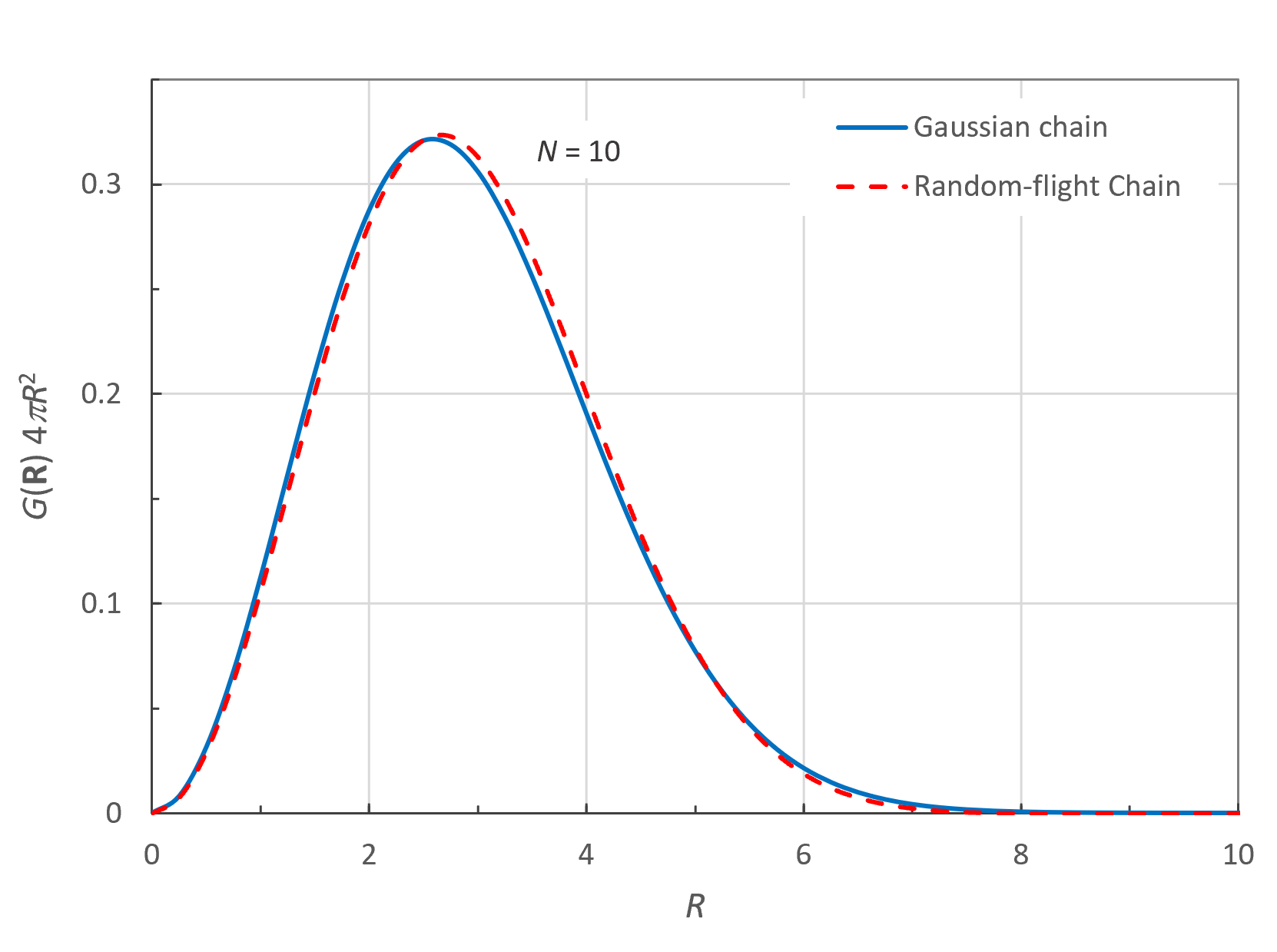
The figure above shows a comparison of the Gaussian distribution function G(R) 4πR² of the end-to-end distance R (full curve) and the corresponding exact distribution function (broken curve) for l = 1 and N = 10. It is seen that even for short chains of only N = 10 segments the asymptotic Gaussian distribution is surprisingly accurate over the whole range. However, the Gaussian distribution has none-zero values (though very small) for R > Nl, where the exact value is zero; Thus, the Gaussian distribution is not valid when R approaches full extension of the chain.

References & Notes

1. The length of a bond is fluctuating around its mean value l due to atomic vibrations in the backbone of the polymer chain.

2. M. Doi, S.F. Edwards, The Theory of Polymer Dynamics, Academic Press, New York (1986)

3. H. Yamakawa, Modern Theory of Polymer Solutions, New York (1971)

4. A. Y.Grossberg, A. R. Khokhlov, Translated by. Y.A. Atanov, Statistical Physics of Macromolecules, Woodbury 1994

5. W. Kuhn and F. Gruen, Kolloid Z., 101, 248-271 (1942).

6. H. M. James and E. Guth, J. Chem. Phys., 11, 455 (1943)

7. L. R. G. Treloar, Trans. Faraday Soc., 42, 77 (1946)

8. M. C. Wang and E. Guth, J. Chem. Phys., 20, 1144 (1952)

9. C. Hsiung, H. Hsiung, and A. Gordus, J. Chem. Phys., 34, 535 (1961)